- Головна сторінка
- Методична скарбничка
- ВІдкриті уроки та відкриті позакласні заходи
- Розробки уроків
- Позакласна робота
- На допомогу учням
- Математика - це цікаво!
- Нормативні документи
- Готуємося до ЗНО та ДПА
- Моя робота класного керівника
- Моє методичне обєднання
- Інтернет- ресурси
- Математики жартують
- Крилаті вислови про математику
- Головоломки ,ребуси
- Підручники,посібники
четвер, 24 березня 2016 р.
вівторок, 22 березня 2016 р.
понеділок, 21 березня 2016 р.
Особливості вивчення математики у загальноосвітніх навчальних закладах у 2015/2016 навчальному році
Додаток до листа Міністерства освіти і науки України від 26.06. 2015 р. № 1/9-305
Особливості вивчення базових навчальних дисциплін у 2015/2016 навчальному році пов’язані, першою чергою, зі змінами, внесеними до навчальних програм.На виконання наказів Міністерства освіти і науки України
від 05.11.2014 № 1275 «Про проведення експертизи та громадського обговорення типових навчальних планів та навчальних програм для початкової школи» та
від 06.02.2015 № 100 «Про розвантаження навчальних програм для учнів 5 – 9 класів загальноосвітніх навчальних закладів» до навчальних програм внесено зміни, спрямовані на їх розвантаження, врахування вікових особливостей розвитку дитини, відповідність сучасному розвитку науки та технологій.
Після громадського обговорення та розгляду Колегією Міністерства зміни до програм були затверджені наказами МОН:
1) № 149 від 22.12.2014 «Про затвердження змін до навчальних програм для 4-х класів загальноосвітніх навчальних закладів» з української мови, літературного читання, математики, природознавства, «Я у світі», інформатики, російської мови для шкіл з російською мовою навчання, української мови для шкіл з навчанням російською мовою;
2) № 584 від 29.05.2015 «Про затвердження змін до навчальних програм для 1-3-х класів загальноосвітніх навчальних закладів» з української мови, літературного читання, математики, природознавства, «Я у світі», інформатики, російської мови для шкіл з російською мовою навчання, української мови для шкіл з навчанням російською мовою;
3) № 585 від 29.05.2015 «Про затвердження змін до навчальних програм для загальноосвітніх навчальних закладів ІІ ступеня», яким затверджено зміни та надано гриф «Затверджено Міністерством освіти і науки» програмам для 5 – 9 класів з таких навчальних предметів: українська мова, українська література, зарубіжна література, іноземні мови, історія України, всесвітня історія, математика, біологія, фізика, хімія, географія, інформатика, трудове навчання, українська мова для шкіл з навчанням російською мовою, українська мова для шкіл з навчанням молдовською мовою, українська мова для шкіл з навчанням румунською мовою, українська мова для шкіл з навчанням польською мовою, українська мова для шкіл з навчанням угорською мовою, болгарська мова для загальноосвітніх навчальних закладів з навчанням українською мовою, мова іврит для загальноосвітніх навчальних закладів з навчанням українською мовою, молдовська мова для загальноосвітніх навчальних закладів з навчанням молдовською мовою, польська мова для загальноосвітніх навчальних закладів з навчанням українською мовою, польська мова для загальноосвітніх навчальних закладів з навчанням польською мовою, російська мова для шкіл з навчанням українською мовою (початок навчання з 1-го класу), російська мова для шкіл з навчанням українською мовою (початок навчання з 5-го класу), російська мова для шкіл з навчанням російською мовою, румунська мова для загальноосвітніх навчальних закладів з навчанням українською мовою (початок вивчення з 1 класу), румунська мова для загальноосвітніх навчальних закладів з навчанням українською мовою (початок вивчення з 5 класу), румунська мова для загальноосвітніх навчальних закладів з навчанням румунською мовою, словацька мова для загальноосвітніх навчальних закладів з навчанням українською мовою, угорська мова для загальноосвітніх навчальних закладів з навчанням угорською мовою, інтегрований курс «Література» (молдовська та зарубіжна), інтегрований курс «Література» (польська та зарубіжна), інтегрований курс «Література» (російська та зарубіжна) для шкіл з навчанням російською мовою, інтегрований курс «Література» (румунська та зарубіжна), інтегрований курс «Література» (словацька та зарубіжна),
Навчальні програми зі змінами розміщено на сайті (http://iitzo.gov.ua/serednya-osvita-navchalni-prohramy/). Програми позбавлені жорсткого поурочного поділу, вчителі можуть обирати послідовність розкриття навчального матеріалу в межах окремої теми, але так, щоб не порушувалась логіка його викладу.
Обласні, районні та міські методичні кабінети (об’єднання) не можуть втручатися в такі питання, оскільки це винятково компетенція вчителя.
Навчально-методичне забезпечення, рекомендоване Міністерством до використання в навчальних закладах, зазначено у Переліках навчальних програм, підручників та навчально-методичних посібників, розміщених на офіційному веб-сайті Міністерства (www.mon.gov.ua).
Дозволяється використовувати підручники з відповідним грифом Міністерства, що видані в попередні роки, враховуючи при цьому зміни у програмах.
Щодо додаткової навчально-методичної літератури, то вчитель вільний у її виборі й може застосовувати таку, що найкраще реалізовує його методику навчання.
Також залишаються актуальними методичні рекомендації Міністерства щодо організації навчально-виховного процесу і вивчення базових дисциплін попередніх років. Тексти методичних рекомендацій розміщені на сайті МОН (http://old.mon.gov.ua/ua/often-requested/methodical-recommendations) та в Інформаційних збірниках Міністерства освіти і науки відповідних років.
Відповідно до наказу МОН України від 08.05.2015 № 518 змінено назву предмета «Світова література» на «Зарубіжна література».
Необхідно також врахувати в роботі листи Міністерства від 3 червня 2014 р. №1/9-282 «Про формування класів з навчанням українською мовою, мовами національних меншин та вивчення цих мов», від 6 червня 2014 р. № 1/9-299
«Про забезпечення права представників кримськотатарського народу на здобуття загальної середньої освіти рідною мовою чи вивчення цієї мови» щодо неприпустимості звуження конституційних прав громадян на здобуття освіти українською мовою, мовами національних меншин чи вивчення цих мов, а також забезпечення освітніх прав представників кримськотатарського народу.
На відміну від підходів до укладання методичних рекомендацій про вивчення предметів, що практикувалися упродовж багатьох років і в яких нерідко з року в рік переповідалися добре відомі вчителям-практикам і методистам загальнодидактичні концепції та підходи до навчання дітей, у цьогорічних рекомендаціях переважно йдеться про нововведення.
Математика
У 2015/2016 навчальному році 7 класи загальноосвітніх навчальних закладів продовжать навчання за програмою «Математика. Навчальна програма для учнів 5–9 класів загальноосвітніх навчальних закладів» (авт. М. Бурда, Ю. Мальований, Є. Нелін, Д. Номіровський, А. Паньков, Н. Тарасенкова, М. Чемерис, М. Якір), затвердженою наказом Міністерства освіти і науки України від 29.05.2015 № 585 «Про затвердження змін до навчальних програм для загальноосвітніх навчальних закладів ІІ ступеня» та розміщеною на сайті Міністерства освіти і науки України (http://old.mon.gov.ua/img/zstored/files/Програма%20Математика%205-9.doc)
Звертаємо увагу, що до навчальної програми з математики внесено зміни, викликані потребою розвантаження навчального матеріалу. Так, з курсу математики в 5-6 класах вилучено елементи комбінаторики й теорії ймовірностей. Учні не зобов’язані більше набувати умінь розв’язувати найпростіші комбінаторні задачі шляхом розгляду можливих варіантів та на прикладах пояснювати поняття випадкової події та ймовірності появи випадкової події.
Програма для 7 класу зазнала таких змін: із курсу геометрії вилучено задачі на побудову, у зв’язку з цим перерозподілено час між темами. Також спрощено державні вимоги до рівня загальноосвітньої підготовки учнів.
За Типовими навчальними планами загальноосвітніх навчальних закладів, затвердженими наказом МОН від 29.05.2014 № 664, на вивчення математики в 7 класі відводиться 4 години на тиждень (2 години алгебри і 2 години геометрії).
В основу побудови змісту й організації процесу навчання математики в 7 класі покладенокомпетентнісний підхід, відповідно до якого кінцевим результатом навчання предмета є сформовані певні компетентності учнів. Їх сутнісний опис подано в програмі в розділі «Державні вимоги до рівня загальноосвітньої підготовки учнів».
Починаючи з 7 класу, вивчаються два математичних курси: алгебра і геометрія.
Основними завданнями курсу алгебри є формування умінь виконання тотожних перетворень цілих і дробових виразів, розв’язування рівнянь і нерівностей та їх систем, достатніх для вільного їх використання у вивченні математики і суміжних предметів, а також для практичних застосувань математичного знання. Важливе завдання полягає в залученні учнів до використання рівнянь і функцій як засобів математичного моделювання реальних процесів і явищ, розв’язування на цій основі прикладних та інших задач. У процесі вивчення курсу посилюється роль обґрунтувань математичних тверджень, індуктивних і дедуктивних міркувань, формування різноманітних алгоритмів, що має сприяти розвитку логічного мислення і алгоритмічної культури школярів.
Основу курсу становлять перетворення цілих раціональних виразів. Важливо забезпечити формування умінь школярів вільно виконувати основні види перетворень таких виразів, що є передумовою подальшого успішного засвоєння курсу та використання математичного апарату під час вивчення інших шкільних предметів.
Істотного розвитку набуває змістова лінія рівнянь та нерівностей. Відомості про рівняння доповнюються поняттям рівносильних рівнянь. Процес розв’язування рівняння трактується як послідовна заміна даного рівняння рівносильними йому рівняннями. На основі узагальнення відомостей про рівняння, здобутих у попередні роки, вводиться поняття лінійного рівняння з однією змінною. Розглядаються системи лінійних рівнянь з двома змінними.
Значне місце відводиться застосуванню рівнянь до розв’язування різноманітних задач. Важливе значення надається формуванню умінь застосовувати алгоритм розв’язування задачі за допомогою рівняння.
У 7 класі вводиться одне з фундаментальних математичних понять — поняття функції. Також вводиться поняття лінійної функції та її графіка. Ці відомості використовуються для графічного ілюстрування розв’язування лінійного рівняння з однією змінною, а також системи двох лінійних рівнянь з двома змінними.
Функціональна лінія пронизує весь курс алгебри основної школи і розвивається в тісному зв’язку з тотожними перетвореннями, рівняннями і нерівностями. Властивості функцій, як правило, встановлюються за їх графіками, тобто на основі наочних уявлень, і лише деякі властивості обґрунтовуються аналітично. У міру оволодіння учнями теоретичним матеріалом кількість властивостей, що підлягають вивченню, поступово збільшується. Під час вивчення функцій значна увага має відводиться формуванню умінь будувати й аналізувати графіки функцій, характеризувати за графіками функцій процеси, які вони описують, спроможності розуміти функцію як певну математичну модель реального процесу.
Головна лінія курсу геометрії — геометричні фігури та їх властивості. Основними поняттями курсу є точка, пряма, площина, належати, лежати між. Перші три поняття — це основні геометричні фігури, а два останніх — основні відношення. Це неозначувані поняття — для них не формулюються означення, але їх зміст розкривається через опис, показ, характеристику. Інші поняття курсу визначаються, а їх властивості встановлюються шляхом доказових міркувань. Учень має усвідомити, що під час доведення теорем можна користуватися означеннями, аксіомами і раніше доведеними теоремами.
Фігури, що вивчаються у 7 класі, — точка, пряма, відрізок, промінь, кут, трикутник, коло, круг. Учень повинен формулювати означення планіметричних фігур та їх елементів, зображати їх на малюнку, класифікувати.
У 7 класі учні ознайомлюються з основами геометричної науки —означеннями, аксіомами, теоремами, основними методами доведення теорем. Поглиблюються і систематизуються відомості про геометричні величини: довжину, градусну міру кута, площу, об’єм.
У навчально-виховному процесі можна використовувати підручники з алгебри та геометрії для 7 класів загальноосвітніх навчальних закладів, що видані в попередні роки і мають відповідний гриф Міністерства освіти і науки України. При цьому слід зважати на особливості нової програми, оскільки вона відрізняється порядком викладення матеріалу і певними спрощеннями.
Під час підготовки вчителів до уроків радимо використовувати періодичні фахові видання: «Математика в рідній школі», «Математика», «Математика в школах України».
Чому не можна ділити на нуль?

«Ділити на нуль не можна!» — Більшість
школярів завчає це правило напам'ять і більше не цікавиться цим
питанням. Всі діти знають, що таке «не можна». Але ж насправді дуже
цікаво і важливо знати, чому ж не можна.
Вся справа в тому, що чотири дії
арифметики — додавання, віднімання, множення і ділення — насправді
нерівноправні. Математики визнають повноцінними тільки дві з них —
додавання і множення. Ці операції та їх властивості включаються в саме
визначення поняття числа. Всі інші дії будуються тим чи іншим чином з
цих двох.
Розглянемо, наприклад, віднімання. Що
значить 5 − 3? Школяр відповість на це просто: треба взяти п'ять
предметів, відняти (забрати) три з них і подивитися, скільки залишиться.
А, от, математики дивляться на це завдання зовсім по-іншому. Немає
ніякого віднімання, є тільки додавання. Тому запис 5 − 3 означає таке
число, яке при складанні з числом 3 дасть число 5. Тобто 5 − 3 — це
просто скорочений запис рівняння: x + 3 = 5. У цьому рівнянні немає
ніякого віднімання. Є тільки завдання — знайти відповідне число.
Аналогічна ситуація з множенням і
діленням. Запис 8 : 4 можна розуміти як результат поділу восьми
предметів за чотирма рівним купках. Але насправді це просто скорочена
форма запису рівняння 4 · x = 8.
Ось тут-то і стає ясно, чому не можна (а
точніше неможливо) ділити на нуль. Запис 5 : 0 — це скорочення від 0 · x
= 5. Тобто це завдання знайти таке число, яке при множенні на 0 дасть
5. Але ми знаємо, що при множенні на 0 завжди виходить 0. Це невід'ємна
властивість нуля, строго кажучи, частина його визначення.
Такого числа, яке при множенні на 0
дасть щось крім нуля, просто не існує. Тобто наша задача не має рішення.
(Так, таке буває, не у всякої задачі є рішення.) А значить, запису 5 : 0
не відповідає жодне конкретне число, і він просто нічого не позначає і
тому не має сенсу. Безглуздість цього запису коротко висловлюють,
кажучи, що на нуль ділити не можна.
Найбільш уважні читачі в цьому місці
неодмінно запитають: а чи можна нуль ділити на нуль? Справді, адже
рівняння 0 · x = 0 успішно вирішується. Наприклад, можна взяти x = 0, і
тоді отримуємо 0 · 0 = 0. Виходить, 0 : 0 = 0? Але не будемо поспішати.
Спробуємо взяти x = 1. Отримаємо 0 · 1 = 0. Правильно? Значить, 0 : 0 =
1? Але ж так можна взяти будь-яке число і отримати 0 : 0 = 5, 0: 0 = 317
і т.д.
Але якщо підходить будь-яке число, то у
нас немає ніяких підстав зупинити свій вибір на якомусь одному з них.
Тобто ми не можемо сказати, якому числу відповідає запис 0 : 0. А раз
так, то ми змушені визнати, що цей запис теж не має сенсу. Виходить, що
на нуль не можна ділити навіть нуль. (В математичному аналізі бувають
випадки, коли завдяки додатковим умовам задачі можна віддати перевагу
одному з можливих варіантів вирішення рівняння 0 · x = 0; в таких
випадках математики говорять про «розкриття невизначеності», але в
арифметиці таких випадків не зустрічається.)
Ось така особливість є у операції ділення. А точніше — у операції множення і пов'язаного з нею числа нуль.
Ну, а найбільш допитливі, прочитавши до
цього місця, можуть запитати: чому так виходить, що ділити на нуль не
можна, а віднімати нуль можна? У певному сенсі, саме з цього питання і
починається справжня математика. Відповісти на нього можна тільки
познайомившись з формальними математичними визначеннями числових множин
та операцій над ними. Це не так уже й складно, але чомусь не вивчається в
школі. Зате на лекціях з математики в університеті вас в першу чергу
будуть вчити саме цьому.
Джерело: http://elementy.ru/email/1530320 (рос.)
Автор: Олександр Сергєєв
Автор: Олександр Сергєєв
Чому в році 365 днів?
Щоб знайти кількість днів у році
треба період обертання Землі навколо Сонця поділити на період обертання
Землі навколо власної осі. Оскільки ми ведемо спостереження із Землі, що
бере участь в декількох нерівномірних обертання, то експериментально
визначити періоди обертань непросто, більш того — вони будуть
непостійними.
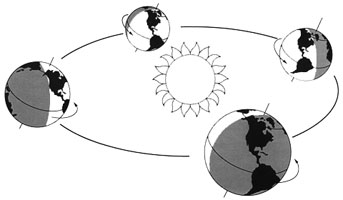
На сьогоднішній день тривалість зоряного
року дорівнює 365,256 середніх сонячних діб. Тривалість року змінюється
через вплив на Землю інших планет сонячної системи. Точні розрахунки
показують, що ексцентриситет орбіти Землі змінюється неперіодично, але з
характерним часом, рівним ста тисячам років.
Тривалість доби також непостійна. Вона
систематично зростає (т. зв. вікові зміни) через гальмування припливами
на 0,0023 сек. у 100 років. У той же час існують стрибкоподібні зміни на
тисячні частки секунди за час у кілька місяців. Достовірно їх причина
не встановлена. Також присутні сезонні зміни через перерозподіл
повітряних і водних мас Землі на ± 0,001 сек. за рік.
Таким чином, кількість днів у році
непостійна. Наприклад, 380 млн років тому в році було близько 400 днів.
Цей результат отриманий після дослідження річних і добових кілець росту
викопних коралів.
Що важче: тонна дерева чи тонна заліза?

Як гадаєте, що важче: тонна дерева чи
тонна заліза? Не поспішайте відповідати, що вага в обох випадках
однакова — подумайте як слід!
Відповідь. Тонна дерева, як це не дивно,
буде, строго кажучи, важчою заліза. Якщо ви згадаєте, закон Архімеда
можна застосувати не тільки до рідин, а й до газів. Кожне тіло «втрачає»
в повітрі зі своєї ваги стільки, скільки важить витіснений ним об'єм
повітря. Дерево і залізо теж втрачають у повітрі частину своєї ваги. Щоб
отримати істинні їх ваги, потрібно цю втрату додати так, що справжня
вага дерева буде дорівнює 1 тонні + вага повітря в об’ємі дерева;
істинна вага заліза дорівнює 1 тонні + вага повітря в об’ємі заліза. Але
тонна дерева займає набагато більший об’єм, ніж тонна заліза, — раз в
15, тому істинна вага тонни дерева більша ваги тонни заліза.
Джерело — «П'ять хвилин на роздуми». Москва 1950. Книга складена за матеріаламиЛ. Успенського, А. Студенцова, Я. Перельмана, Ігнатьєва та ін
Цікаві факти про видатних математиків
Зазирнемо в дитинство окремих видатних математиків.
Жан Д'Aламбер (Лерон).
Початок його життя, як у поганому романі: листопад, ніч, мороз,
заметіль. На східцях церкви св. Жана лежав маленький згорточок, що
тихенько здригався і попискував. Його знайшов поліцейський, який
побачив, що було немовля в дорогій ковдрі. Виявилось, що це був хлопчик.
Його віддали на виховання у багатодітну сім'ю скляра. Хлопчика назвали
Жаном Пероном (тобто Жаном Круглим) за іменем церкви, де його знайшли.
Ставши дорослим, він сам собі вигадав ім'я: Жан Лерон Д'Аламбер.
Нікколо Тарталья.
Справжнє прізвище вченого — Фонтана. Народився у бідній родині. Коли
місто окупували французи, батько Нікколо загинув. Солдати грабували,
палили, вбивали. Маленького Нікколо тяжко поранили і викинули у вікно,
при цьому пошкодили йому щелепу, у нього був розсічений язик. Матері
пощастило врятувати життя сина, але вільно говорити Нікколо вже не зміг,
мова його була вкрай незрозумілою, від чого він і дістав прізвисько
Тарталья, тобто заїка.
По-різному відомі математики здобували освіту.
Більшості з них пощастило навчатися у кращих вчителів, у престижних
школах. Великий вплив на своїх дітей мали їхні освічені батьки. Але
багато хто не мав такої можливості через злидні та інші труднощі, а тому
таким дітям довелося здобувати освіту самотужки. Візьмемо, наприклад,
одну з шкіл.
Піфагорійський союз.
Цей союз був одночасно і філософською школою, і політичною партією, і
релігійним братством. Статут піфагорійського союзу був дуже суворим.
Кожний, хто вступав до нього, відмовлявся від особистої власності на
користь союзу, зобов'язувався не проливати крові, не вживати м'ясної
їжі, берегти таємницю вчення свого вчителя. Членам школи заборонялось
навчати інших за винагороду.
Для стародавніх греків математика була насамперед геометрією. А тому над дверима Академії, де Платон навчав своїх учнів, було зроблено напис: «Нехай сюди не входить ніхто, хто не знає геометрії».
Одного разу цар Птолемей запитав у Евкліда, чи немає в геометрії коротшого шляху для її вивчення, ніж той, що пропонує Евклід. На що вчений відповів: «Для царів немає окремого шляху в геометрії».
Про феноменальну пам'ять Пуссена
існує легенда: однієї безсонної ночі він обчислив у пам'яті 27 цифр
квадратного кореня із 53-цифрового числа, а ранком записав їх.
Обдаровані від природи діти з'являються у всі часи і серед всіх народів:
Дазе називали людиною-рахівником. У 15 років він виступав перед публікою.
Боголюбов у 14 років став студентом Академії наук.
Ейлер у 20 років дістав запрошення до Петербурзької Академії наук, у 26 років його обрали академіком.
Гамільтон у 3 роки читав, у 5 років знав три мови, у 10 років став студентом, у 12 років знав 12 мов, у 22 роки став професором.
Фрідман займався наукою у 6 класі.
Грін, навпаки, тільки у 40 років вступив до університету.
Деякі жадібні до знань діти, не маючи можливості здобути світу, були самоучками. Ось деякі факти.
Тарталья через бідність
залишив школу, вивчивши абетку тільки до букви К. Потім самостійно
опанував грамоту, оволодів латиною і грецькою мовою, математикою. Не
маючи паперу для вправ, він свої записи обчислення робив на надгробках
одного із затишних кладовищ.
Софі Жермен батьки не дозволяли займатися математикою, якою вона захоплювалась. Софі писала свої виклади таємно ночами під ковдрою.
Еварист Галуа, ще коли
був хлопчиком, прочитав першу математичну книжку, що потрапила до його
рук, – це була «Геометрія» Лежандра. Прочитав її так, як інші читають
роман.
Щодо здоров'я великих вчених:
одні вчені мали добре здоров'я, інші хворіли (хто з дитинства, хто уже в
зрілому віці). Є серед вчених і довгожителі, і ті, хто пішов з життя в
ранньому віці, дехто від хвороб, які тоді були невиліковні.
Є вчені, які померли своєю смертю, а є й ті, що загинули насильницькою смертю.
Загинули від хвороби:
- від запалення легенів – Декорт, Больцано, Ковалевська;
- від чуми – Шикард;
- від серцевого нападу – Лузін;
- від злиднів і хвороб – Абель;
- у стані, близькому до психозу, – Больяй.
Померли насильницькою смертю: Піфагор –
випадково під час повстання: Архімед – від руки римлянина під час облоги
Сиракуз: Гіпатія – вбили християнські фанатики; Вільмес – спалили
інквізитори; Банах – загинув у фашистських застінках; Галуа – загинув на
дуелі в 20 років, Ляпунов – самогубство. Ось деякі витяги з цього
приводу.
Нестриманість і дратівливість Больяя,
успадковані ним від матері, спричиняли його сварки з товаришами, які
закінчувалися поєдинками. Було навіть таке, що одного дня його викликали
на дуель відразу 12 офіцерів.
У 24 роки Паскаля розбив параліч (в
дитинстві його покусав скажений пес). Він ледве пересувався на милицях,
але й далі працював. Здавалося, дух цієї людини переміг її немічну
плоть. Потім здоров'я Паскаля то поліпшувалось, то погіршувалось. Коли
йому стало краще, він зібрався одружитися, але нещасний випадок (карету
понесли коні) зовсім вибив Паскаля із нормального життя. З цієї миті,
можна вважати, він помер, хоча прожив іще 8 років. Він сидів одягнений у
волосяницю, утикану цвяхами, жовтий, худий, мовчазний. Паскаль помер на
39-му році життя.
Під час німецької окупації Стефана
Банаха замучили фашисти: його кинули до в'язниці, де вчений був
використаний як донор для годування вошей з метою виготовлення
протитифозної сироватки.
Окремо слід поговорити про довгожителів
серед вчених математиків. Якщо за точку відліку взяти 70 років, то до
цього віку і довше дожили такі вчені, як: Кулик, Вінер, Лейбніц (по 70
років); Фішер (72); Чаплигін (73); Кардано і Архімед (по 75); Ейлер
(76); Гулак (77); Лагранж (77); Галілей (78); Платон (80); Вівіані (81);
Жордан (84); Діофант (84); Пуссен (87); Гаусс (88); Піфагор (90); Фалес
(до 100 років).
Математика ставала в нагоді вченим при виконанні складних завдань у різні часи.
Знання математики допомогли французу Вієту
розкрити шифр у листуванні іспанського короля Філіппа II під час війни
Франції з Іспанією, чим він прискорив перемогу Франції. За це іспанська
інквізиція оголосила Вієта чаклуном і боговідступником і присудила його
до спалення на вогнищі.
Архімед за допомогою
математичних розрахунків сконструював силу-силенну всіляких механізмів,
які настільки допомагали у війні проти римлян при облозі Сиракуз, що Марцелло вимушений був сказати: «Треба припинити війну проти геометра». Пізніше тільки зрада допомогла римлянам увійти до Сиракуз.
Для багатьох вчених математика була сенсом життя.
Тяжкохворий Боссю так
ослаб, що не подавав ніяких ознак життя. Коли над ним схилились його
друзі, які вже думали, що він помер, один з них зауважив: «Зачекайте!
Боссю, скажи, скільки буде сім помножити на дев'ять?». Тяжкохворий, не
розплющуючи очей, ледь чутно сказав: «63». Друзі зраділи: «Раз обчислює, значить живе».
Тяжкохворому Вороному забороняли займатися
обчисленням і взагалі математикою. Він і сам розумів, що не повинен
цього робити, та водночас казав лікарям: «Як ви не розумієте, що заняття
математикою – це і є життя, а інакше для чого ж тоді жити».
Коли на одній вченій раді постало питання, якому предмету у програмах віддати перевагу – мові чи математиці, піднявся мовчазний Гіббс і сказав: «Математика – це мова».
Про те, що математика може все, влучно сказав Чаплигін у розмові з майбутніми інженерами: «Вивчайте математику, все будете знати».
Штейнгауз зазначав, що коли двом різним людям доручити виконати якусь одну справу, то її краще зробить математик.
Вчені-математики за різних часів не
знаходилися осторонь політичних подій, вони брали в них активну участь.
Деякі виступали проти релігії, проти існуючого уряду і потерпали від
цього.
Больцано виступав проти уряду. За ці виступи його звільнили з роботи, віддали під нагляд поліції.
Галуа був
революціонером, публічно виступав проти королівського режиму. Його
супротивники призвели до ситуації, що спричинила дуель, на якій він і
загинув у 20 років, встигнувши за свій короткий вік зробити дуже багато в
царині математики.
Марков (батько) виступав проти царських сатрапів.
Лузін був революціонером.
Галілей під натиском
інквізиції відрікся від «єресі Коперніка», і ще ходить легенда, що,
піднімаючись з колін, він сказав: «А все ж таки вона обертається» (маючи
на увазі Землю).
Вільмес Паоло мав
необережність у присутності інквізитора Торквемади сказати, що він знає,
як розв'язуються рівняння четвертого степеня, які, за словами
Торквемади, самим Богом були заховані від людей. За це Паоло було
заарештовано, після страшних тортур його спалили за вироком іспанської
інквізиції.
Шикарда за винахід лічильної машини (арифмометра) інквізиція засудила до церковного каяття. Машину спалили.
Лобачевському за його атеїзм, волелюбний характер загрожували бути звільненим з університету і відданим у солдати.
Ейнштейну за часів перебування Гітлера при владі винесли заочно смертний вирок.
Янішевський відмовився прийняти присягу на вірність австрійському уряду, змушений був переховуватись.
Платона правитель Сиракуз Діонісій-старший продав у рабство.
Гіпатію з Александрії християнські фанатики вбили за те, що вона не прийняла їхньої віри.
На прикладах з життя видатних учених слід вчитися виховувати у собі чуйність, людяність, мужність.
Безу повинен був
прийняти екзамен у двох своїх учнів, що захворіли на віспу. Сам Безу не
хворів на віспу і дуже цього боявся. Але розумів і те, що коли учні не
складуть іспит, то втратять рік навчання. Забувши про свої страхи, він
поїхав до хворих, проекзаменував їх і був задоволений, бо його жертва не
була марною.
Лобачевський помітив в одній із крамниць хлопчика,
який кожної вільної хвилини щось обчислював. Як виявилось, це був
сирота, якого господар привіз з Італії. На запитання Лобачевського, чи
хоче хлопчик навчатися, той з радістю відповів: «Так». Лобачевський
домовився з господарем і, забравши хлопчика, віддав його до гімназії.
Закінчивши гімназію, здібний учень закінчив і університет. У майбутньому
він став професором фізики. Янішевський роздавав бідним свій одяг,
згодом на власні кошти відкрив притулок для сиріт і весь час утримував
його. Після смерті своє тіло заповідав віддати до університетської
клініки.
Математика – чудова наука.
Олександр з Вільдьє написав пісню про алгоритм, яка складається з 2645 віршів.
Леонардо да Вінчі назвав механіку «раєм математичних наук».
У XV ст. арифметику називали «малим мистецтвом», а алгебру – «великим мистецтвом».
Ньютон сказав про
математику, що вона подібна до сварливої жінки, якщо хто захоче з нею
поспілкуватися, то повинен весь час сперечатися.
Магницький одержав своє прізвище від Петра І за велике прaгнення до математики.
Бурбакі – це псевдонім, під яким виступала ціла група вчен математиків.
Лагранжа за велику ерудицію Наполеон назвав «Хеопсовою пiрамідою математичних наук».
Гаусса називали «королем математики» навіть його сучасники.
Вієта називали «батьком алгебри».
Вінера називали «батьком кібернетики».
Цікаві факти про математику

Чому Нобелівська премія не вручається за досягнення в математиці?
Існує думка, що Альфред Нобель
не включив математику в список дисциплін своєї премії через те, що
його дружина зрадила його з математиком. Насправді Нобель ніколи не був
одружений. Справжня причина ігнорування математики Нобелем невідома,
але є кілька припущень. Наприклад, на той момент вже існувала премія з
математики від шведського короля. Інша — математики не роблять важливих
винаходів для людства, так як ця наука має чисто теоретичний характер.
Чим наше число нуль відрізняється від західного?
У нашій математичній літературі нуль не є натуральним числом, а в західній, навпаки, належить до множини натуральних чисел.
Коли святкують день числа Пі?
У числа Пі є два неофіційних свята.
Перше — 14 березня, оскільки цей день в Америці записується як 3.14.
Друге — 22 липня, яке в європейському форматі записується 22/7, а
значення такого дробу є досить популярним наближеним значенням числа
Пі.
Хто вирішив складну математичну проблему, прийнявши її за домашнє завдання?
Американський математик Джордж Данціг,
будучи аспірантом університету, одного разу спізнився на урок і
прийняв написані на дошці рівняння за домашнє завдання. Воно здалося
йому складніше звичайного, але через кілька днів він зміг його
виконати. Виявилося, що він вирішив дві «нерозв’язані» проблеми в
статистиці, над якими билося багато вчених умів.
Який математик осягав основи науки по шпалерах в кімнаті?
Софія Ковалевська
познайомилася з математикою в ранньому дитинстві, коли на її кімнату
не вистачило шпалер, замість яких були наклеєні листи з лекціями
Остроградського про диференціальне та інтегральне числення.
Яка гра пов’язана з «числом диявола» («число звіра»)?
Сума всіх чисел на рулетці в казино дорівнює числу диявола — 666.
Де намагалися законодавчо округлити число Пі?
У штаті Індіана в 1897 році був
випущений білль, який мав законодавчо встановити значення числа Пі
рівним 3,2. Даний білль не став законом завдяки своєчасному втручанню
професора університету.
Який математичний закон розкривається в теоремі про двох міліціонерів?
Деякі математичні закони називають по
аналогії із ситуаціями в реальному житті. Наприклад, теорема про
існування границі функції, яка «затиснута» між двома іншими функціями,
що мають однакову границю, називається теоремою про двох міліціонерів.
Це пояснюється тим, що якщо два міліціонера тримають між собою злочинця
і при цьому йдуть в камеру, то ув’язнений також змушений йти туди.
Який знак замість плюса використовують учні ізраїльських шкіл?
Релігійні євреї прагнуть уникати
християнської символіки і взагалі знаків, схожих на хрест. Наприклад,
учні деяких ізраїльських шкіл замість знака «плюс» пишуть знак, що
повторює перевернуту букву «т».
Найбільше просте число
Нагадаю, що простими числами називають числа, які мають лише два дільники - одиницю і самого себе.
Зрозуміло, що простих чисел є нескінченна кількість. Але , може, все ж є
найбільше? Пошуки найбільшого простого числа не припиняються. І ось
нове відкриття! Нещодавно було знайдено нове найбільше просте число,
довжина якого складає 17425170 цифр. Це число стає володарем рекорду,
відібравши пальму першості у кількості, довжиною 12978189 цифр,
знайденого ще в 2008 році. Значення числа-рекордсмена є двійка в степені
57885161 мінус один, воно було знайдене вченим-математиком Кертісом
Купером (Curtis Cooper) з університету Центральної Міссурі (University
of Central Missouri) за допомогою мережі комп’ютерів GIMPS, що працюють
по технології розподілених обчислень. Цей проект використовує
обчислювальну потужність комп’ютерів добровільних учасників і багато в
чому нагадує проект SETI @ Home, який займається обробкою даних,
отриманих від радіотелескопу проекту Search for Extraterrestrial
Intelligence (SETI).
У складі мережі GIMPS (Great
Internet Mersenne Prime Search) знаходиться безліч комп’ютерів з 360
тисячами обчислювальних ядер, що забезпечує сумарну обчислювальну
потужність мережі 150 трильйонів операцій на секунду. І число-рекордсмен
– це вже третє велике просте число, виявлене Купером за допомогою
мережі GIMPS. “Пошук простих чисел нагадує підйом на гору Еверест” –
розповідає Джордж Уолтмен (George Woltman), програміст з Флориди, який
працював над створенням мережі GIMPS, – “Люди займаються цим виключно
заради відкриття того, що було раніше невідомо”.
Крім усього іншого нове число є
48-м числом ряду рідкісних чисел, званого простими числами Мерсенна .
Всі числа Мерсенна мають значення рівні зведеної в яку-небудь ступінь
двійки мінус один. З того моменту, коли цей ряд чисел був описаний
французьким монахом-математиком Марену Мерсенна (Marin Mersenne) 350
років тому, були виявлені всього 48 чисел цього ряду, включаючи і
нещодавно відкрите число.
Після виявлення нового числа
Мерсенна його значення було перевірене ще декількома іншими
вченими-математиками за допомогою інших обчислювальних систем і
суперкомп’ютерів.
Найпростішим і інтуїтивним
методом пошуку простих чисел є послідовний розподіл числа-кандидата на
числа з меншим значенням, але такий підхід вимагає величезної кількості
розрахунків і витрат обчислювальних потужностей. “Якщо піти таким
шляхом, пошук нового числа зайняв би більше часу, ніж вік всього
Всесвіту” – розповідає Джордж Уолтмен. Замість цього математики
використовували набір складних алгоритмів, використання яких дозволило
різко скоротити час, потрібний для пошуків числа.
Відкриття нового числа Мерсенна
робить Кертіса Купера кандидатом на отримання премії GIMPS, сума якої
правда невелика і складає 3000 доларів.
А. може, й серед вас знайдеться хтось, хто насмілиться на новий рекорд?
середа, 16 березня 2016 р.
Цікавинки математики
Математичні знаки «+» і «-»
1.
Сучасні знаки «+» і «-» стали загальновизнаними, починаючи з XVII ст. Вперше ці
знаки з'явилися в праці Лейпцігського професора Й.Відмана (1489). Вважають, що
знаки «+» і «-» виникли з торговельної недостачі, збитку, а знак «+» для
позначення прибутку.
2.
Математичні знаки «+» і «-» прийшли до нас із країн Сходу. Арабські вчені,
виводячи правила дій з додатними й від'ємними числами, користувались такими
цікавими аналогіями. «Друг мого друга мій друг» (помноживши «плюс» на «плюс»,
дістанемо «плюс»); «Ворог мого ворога — мій друг» (помноживши «мінус» на
«мінус», дістанемо «плюс»); «Ворог мого друга - мій ворог» (помноживши «плюс»
на мінус, і навпаки, дістанемо «мінус»).
Історія знака ділення
У різні часи дію ділення записували по різному. Довгий
час спочатку записували дільник, потім ділене, а замість знака ділення писали
дужки, Араби, а пізніше і європейці для позначення ділення писали горизонтальну
риску. Фламандський математик Сімон Стевін (XVI ст.) як знак ділення
застосовував букву О. Дві крапки як знак ділення запропонував Лейбніц (1684
р.).Терміни «ділення», «ділене», «дільник» в сучасному розумінні почали
вживати в X ст. Результат ділення ще довго називали «сумою ділення». Термін
«частка» з'явився в XIII ст. в італійського математика Леонардо Пізанського.
Основна властивість частки (легенда)
В одному королівстві, де царицею при дворі була
Математика, служили чотири придворні Дами: Сума, Різниця, Добутка і Частка.
Сума і Добутка
це Дами,
найбільш улюблені Царицею. Вони мали свої права, якими користувалися:
переставний, сполучний, розподільний закони. Різниця, менш любима, не
відставала від них, бо була учасницею розподільного закону та й частково
сполучного. Лиш Частка, наймолодша Дама королівства, не мала таких прав, якими
користувалися інші три. Скромність заважала їй сказати про це Цариці, то
жилось їй поки що так собі. Незважаючи на все це, Частка на совість служила
повелительці і виконувала всі її розпорядження при діленні.
Одного разу Математика захворіла дуже важкою хворобою.
Та так захворіла, що ніхто не сподівався на її одужання Королівство почало
розорятися. Сума, Різниця, Добутка залишили хвору Царицю, лиш Частка
залишилась при дворі й піклувалась про хвору, сама варила та подавала ліки з
трав. І сталося диво — Цариця одужала і віддячила Частці за її відданість.
Лише одній їй дала основну властивість частки (закон), якої не має ніхто. Ця
властивість ствержує: ділене і дільник можна ділити або множити на одне й те
саме число (відмінне від нуля), і частка при цьому не зміниться.
Точка й пряма. Відрізок. Промінь (казка)
Жив собі маленький відрізок, нетямущий та обмежений.
Та як же йому розвиватися, якщо не бачить далі від своїх кінців? Одного разу
мати Пряма зварила варення і поставила на полицю, сказавши си- ну:«Дивись,
синку, це варення чарівне. Якщо з'їси його більше, ніж одну ложку, то буде
біда.» Але відрізок Не послухав матері, дочекався, коли вона піде — і наївся
варення досхочу. І раптом він почав рости й виріс до безмежної висоти. Другого
його кінця не стало зовсім видно — він перетворився у Промінь. Заплакав
Промінь, його сльози, що падали згори, були схож< на дощ. Мати хотіла
вилікувати свого сина. Що тільки з ним не робили: й рубали, й пиляли — все
даремно. Одного разу проходила повз них Точка. Дізнавшись, у чому річ, вона
взялася допомогти. Точка стала на Промінь, і він знову перетворився на Відрізок
та повернувся додому.
Число Пі
1. Назва числа Пі пішла від першої букви
грецького слова «периферія», що означає коло. А його значення допоможе
запам'ятати така приказка: «Ось і кола, і круги намалюємо та лічити цифри
пропонуємо». Якщо виписати кількість букв у кожному слові, дістанемо
3,1415926... Існує і віршик, в якому запам'ятати число допомагає рима:
То не
важка буде праця —
«пі»
роздивитися зблизька:
Три,
чотирнадцять, п'ятнадцять,
Дев'ять,
ще двійка й шістка.
2. У 1992
році число Пі обчислили з точністю до 1 мільярда 11 мільйонів 196
тисяч 691 знака після коми. Цей факт занесено у Книгу рекордів Гіннеса. Саме
число Пі з такою точністю, туди не занесли,
бо для його запису знадобилося б понад тисячу сторінок.
Теорема Піфагора (казка)
В одному із грецьких міст жили двоє нерозлучних
друзів, і кожен з них мав ім'я Катет. Дружили вони ще з раннього дитинства і
поклялися, що ніхто в житті, хоч би як воно не складалося, не заважатиме їхній
дружбі. Були вони обидва скромні, чесні хлопці, навіть мали однакові
уподобання. Одного разу зустріли вони дівчину на ім'я Гіпотенуза і полюбили
її. Дівчина була дуже гарна: висока, струнка, з довгим чорним волоссям та
виразним милим обличчям. Не знала вона кому із хлопців віддати перевагу, бо
подобались вони їй обидва. Кожен із хлопців мріяв про Гіпотенузу, та не хотів
ставати на перешкоді своєму другові. І ось, незалежно один від одного, пішли
друзі із міста, щоб не заважати. Один думав так: «Піду к звідси, адже Катет мій
друг, і я хочу, щоб він був щасливий. Не заважатиму його щастю — нехай він
зостається з Гіпотенузою». Такі ж думки були і в іншого Катета.Один із хлопців
пішов на північ, другий — на схід. Хоч розійшлися вони і далеко були один від
одного, та зв'язує їх думка про Гіпотенузу. Тому теорема: «Катет2 +
Катет2 = Гіпотенуза2», — ніби схрещені шпаги у бою між двома Катетами через Гіпотенузу.
Підписатися на:
Коментарі (Atom)















